| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 대학생
- LIFO
- 코뮤니티
- 코딩
- 코딩좀알려주라
- IT
- 큐
- O(1)
- 양방향 연결 리스트
- 스택
- 한국외대
- 프로그래밍
- 한방향 연결 리스트
- 웹 기초
- 시간 복잡도
- 알고리즘
- 동적 배열
- 수파자
- 대외활동
- FIFO
- 한국대학생IT경영학회
- 선형 자료 구조
- 모각코
- 자료구조
- 서포터즈
- 리스트
- CSS
- HTML
- 파이썬
- 연결 리스트
- Today
- Total
대학생 쩡딱구리
4-1. 한방향 연결 리스트 본문
그동안 동적 배열과 동적 배열을 기반으로 한 자료구조를 다루었다. 하지만 동적 배열엔 아래와 같은 단점이 있다.
- 동적 배열의 길이가 저장하는 요소의 수보다 길다. 즉 메모리 낭비가 있다.
- 분할 분석 방식이 실시간 시스템에서 허용되지 않을 때가 있다.
- 배열의 삽입 또는 삭제 연산 비용이 O(n)으로 비싸다. 삽입, 삭제 연산이 중요할 경우 문제가 될 수 있다.
동적 배열의 이러한 단점을 해소해 삽입/연산을 빠르게 할 수 있는 선형 자료구조가 연결 리스트이다.
1. 연결 리스트란?

연결 리스트는 분산 관리 방식 자료구조이다. 이 말은 각 요소 별로 노드를 할당해 관리한다는 의미이다. 연결 리스트는 노드가(node)가 링크(link)로 연결된 순차 자료 구조로, 요소의 접근이 느리지만(O(n)) 삽입/삭제 연산은 O(1)으로 빠르다.
다시 말하면 연결 리스트는 추가/삭제 연산을 빠르게 만든 동적 집합 관리 자료구조이다.
2. 한방향 연결 리스트
위의 사진처럼 노드들이 한 방향으로만 연결된 연결 리스트를 한방향 연결 리스트(Singly Linked List)라고 한다. 한 방향 연결 리스트에서 element는 객체의 레퍼런스, next는 다음 노드의 레퍼런스(링크)이다. 각 노드는 객체와 다음 노드의 레퍼런스인 링크를 저장하며, 링크를 따라 특정 노드의 데이터를 접근하고 수정한다. 한방향 연결 리스트의 특징을 살펴보자.
1) 가변 크기

한방향 연결 리스트는 미리 고정된 크기로 할당되는 구조가 아니라 필요할 때마다 노드(E)가 할당된다. 따라서, 요소(element) 수에 비례해 공간을 사용한다.
2) 추가 및 삭제: 한방향 연결 리스트는 주소만 변경하면 삽입/삭제가 가능한 구조이다.

3) 순회(traverse): 한방향 연결 리스트는 Head부터 Tail까지 노드의 링크를 따라 순회하며 특정 노드를 접근한다.

한방향 연결 리스트는 링크를 따라 한 노드씩 이동하는 방식이다. 첫 번째 노드를 Head, 마지막 노드를 Tail로 설정했을 때 Tail은 next가 None이라는 것으로 판단하며 일반적으로 Head와 함께 Tail도 저장해 관리한다.
3. SinglyLinkedList 클래스
전체 코드를 본 후 부분별로 나누어 설명한다.
# Node 클래스
class _Node:
def __init(self, element=None, next=None):
self._element = element # 노드에 저장되는 element 값
self._next = next # 다음 노드로의 링크(초기값은 None)
def __str__(self):
return str(self._element) # 출력 문자열 (print(node)에서 사용)
class SinglyLinkedList:
def __init__(self):
self._head = None # 연결 리스트의 가장 앞의 노드(head)
self._size = 0 # 리스트의 노드 개수
def __len__(self):
return self._size # len(A) = A의 노드 개수 리턴
def print_list(self):
v = self._head
while(v):
print(v._element, "->", end = "")
v = v._next
print("None")
def add_first(self, element):
newest = self._Node(element, self._head) # 새 노드 생성
self._head = newest
self._size += 1
def add_last(self, element):
newest = self._Node(element) # 새 노드 생성
if self._head == None: # empty list
self._head = newest
else:
tail = self._head
while tail._next != None:
tail = tail._next
tail._next = newest
self._size += 1
def remove_first(self):
# head 노드의 값 리턴. empty list이면 None 리턴
if self._head == None: # empty list
return None
element = self._head._element
self._head = self._head._next
self._size -= 1
return element
def remove_last(self):
# tail 노드의 값 리턴
# empty list이면 None 리턴
if self._head == None:
return None
prev = None
tail = self._head
while tail._next != None:
prev = tail
tail = tail._next
if prev == None:
self._head = None
else:
prev._next = None
self._size -= 1
return tail._element
def search(self, element):
# element 값을 저장된 노드 리턴, 없으면 None 리턴
v = self._head
while v:
if v._element == element: return v
v = v._next
return None
def __iter__(self): # generator 정의
v = self._head
while v != None:
yield v
assert isinstance(v._next, object)
v = v._next
def search(self, element):
for v in self:
if v._element == element:
return v
return None
def remove(self, element):
# 노드 x를 제거한 후 True 리턴, 제거 실패면 False 리턴
x = self.search(element)
if x == None or self._size == 0:
return False
if x == self._head:
self.remove_first()
else:
prev = self._head
while prev._next != x:
prev = prev._next
prev._next = x._next
self._size -= 1
return True
Node 클래스 선언
1) 클래스 선언
# Node 클래스
class _Node:
def __init(self, element=None, next=None):
self._element = element # 노드에 저장되는 element 값
self._next = next # 다음 노드로의 링크(초기값은 None)
2) 객체의 문자열 표현
def __str__(self):
return str(self._element) # 출력 문자열 (print(node)에서 사용)
SinglyLinkedList 클래스
1) 클래스 선언
- self._head: head node 관리(단, Tail을 별도로 관리하지는 않음)
- self._size: 길이 정보를 빠르게 제공하기 위해 별도로 관리
class SinglyLinkedList:
def __init__(self):
self._head = None # 연결 리스트의 가장 앞의 노드(head)
self._size = 0 # 리스트의 노드 개수2) 리스트에 저장된 요소의 개수: self._size 리턴
def __len__(self):
return self._size # len(A) = A의 노드 개수 리턴3) 출력: Head에서 Tail까지 link를 따라가며 element를 출력
def print_list(self):
v = self._head
while(v):
print(v._element, "->", end = "")
v = v._next
print("None")4) 추가
- Head에 새로운 요소 추가

def add_first(self, element):
newest = self._Node(element, self._head) # 새 노드 생성
self._head = newest
self._size += 1
- Tail에 새로운 요소 추가: 빈 리스트인 경우 새로운 노드가 head가 되며 노드가 하나 이상인 경우 tail까지 이동을 해서 끝에 추가한다.

def add_last(self, element):
newest = self._Node(element) # 새 노드 생성
if self._head == None: # empty list
self._head = newest
else:
tail = self._head
while tail._next != None:
tail = tail._next
tail._next = newest
self._size += 15) 삭제
- Head의 요소 삭제

def remove_first(self):
# head 노드의 값 리턴. empty list이면 None 리턴
if self._head == None: # empty list
return None
element = self._head._element
self._head = self._head._next
self._size -= 1
return element
- tail의 요소 삭제
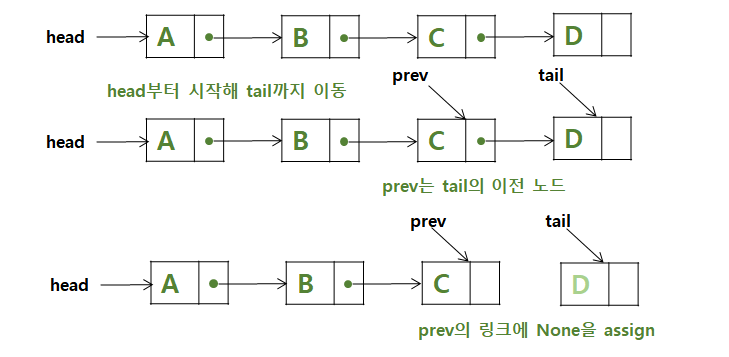
def remove_last(self):
# tail 노드의 값 리턴
# empty list이면 None 리턴
if self._head == None:
return None
prev = None
tail = self._head
while tail._next != None:
prev = tail
tail = tail._next
if prev == None:
self._head = None
else:
prev._next = None
self._size -= 1
return tail._element6) 검색
- head 노드부터 tail까지 링크를 따라가면서 찾는 방법.
- key와 같은 값을 갖는 노드를 찾으면 노드를 return
- key와 같은 값을 갖는 노드를 못 찾으면 tail의 next까지 가게 되므로 None을 return
def search(self, element):
# element 값을 저장된 노드 리턴, 없으면 None 리턴
v = self._head
while v:
if v._element == element: return v
v = v._next
return None
- generator 정의
- __iter__함수를 구현하여 generator로 정의.
- 매번 iter를 호출하면 값을 외부로 전달하고 yield 전까지만 실행
def __iter__(self): # generator 정의
v = self._head
while v != None:
yield v
assert isinstance(v._next, object)
v = v._next
- for loop로 검색: 클래스를 iterable로 정의했다면 for loop를 통해 찾을 수 있음.
def search(self, element):
for v in self:
if v._element == element:
return v
return None
7) 삭제

- prev는 노드 x 이전 노드
- 노드 x를 발견할 때까지 prev를 이동하다가 발견되면 prev.next를 x.next로 연결
def remove(self, element):
# 노드 x를 제거한 후 True 리턴, 제거 실패면 False 리턴
x = self.search(element)
if x == None or self._size == 0:
return False
if x == self._head:
self.remove_first()
else:
prev = self._head
while prev._next != x:
prev = prev._next
prev._next = x._next
self._size -= 1
return True
4. 성능 분석
연결 리스트로 큐를 구현하면 모든 연산이 O(1) 시간 복잡도를 갖는다.
| Operation | Running Time | Dynamic Array와의 비교 | |
| L.add_first(e) | O(1) | O(n) | data.insert(k, value) |
| L.add_last(e) | O(n) | O(1) | data.append(value) |
| L.remove_first() | O(1) | O(n) | data.pop(k) |
| L.remove_last() | O(n) | O(1) | data.pop() |
| L.remove(e) | O(n) | O(n) | data.remove(value) |
| L.search(e) | O(n) | O(n) | |
| len(L) | O(1) | O(1) | |
| L.printlist() | O(n) | O(n) | |
다음 게시글에선 연결 리스트로 구현한 스택과 큐, 원형 연결 리스트에 대해 다룬다.
'STUDIES > DATA STRUCTURE' 카테고리의 다른 글
| 4-3. 원형 연결 리스트 (0) | 2020.10.21 |
|---|---|
| 4-2. 연결 리스트로 스택, 큐 구현하기 (0) | 2020.10.21 |
| 3-3 덱 (0) | 2020.10.17 |
| 3-2. 큐 (0) | 2020.10.17 |
| 3-1. 스택 (0) | 2020.10.17 |
